かっこいい!世界一美しい数式ランキングTOP10
みなさん、こんにちは!数学と物理の世界には、一見すると美しくは見えない謎めいた数式がたくさんありますよね。でも、その奥をのぞいてみると、深遠な真理を明らかにし、私たちの世界観をがらりと変えてしまうほどの「美しさ」を秘めているものが存在します。今回は、そんな魅惑の数式たちを、ランキング形式でご紹介!美しさと奥深さの両方を楽しんでいただければ幸いです。
第10位:微積分の基本定理(Fundamental Theorem of Calculus)
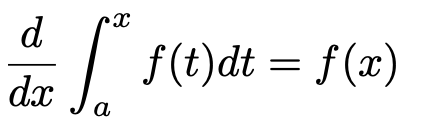
「積分と微分が実は表裏一体だった!」という衝撃的な事実を教えてくれるのが、この数式。ある区間の積分(グラフの面積)と、その区間における微分(変化率)が密接につながっている、という数学界の不思議。私たちが計算をするとき、道具としては当たり前に使っている微分積分が、こんなにも優雅な形でまとまっているというのは実に感慨深いですよね。
第9位:シュレディンガー方程式 (Schrödinger Equation)
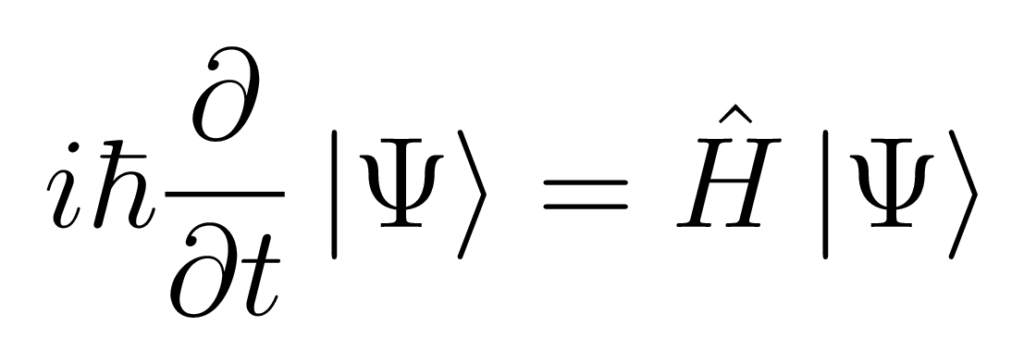
量子力学の代名詞ともいえる「シュレーディンガー方程式」は、「粒子なのか波なのか分からない!」という量子の不思議な振る舞いを記述するための方程式。波動関数と呼ばれる関数を使い、電子などのミクロな世界を見事に表現します。猫が生きているか死んでいるか両方の状態にある?なんていう量子の世界観を語るうえで欠かせない存在です。
第8位:オイラー数 (Euler’s Number)
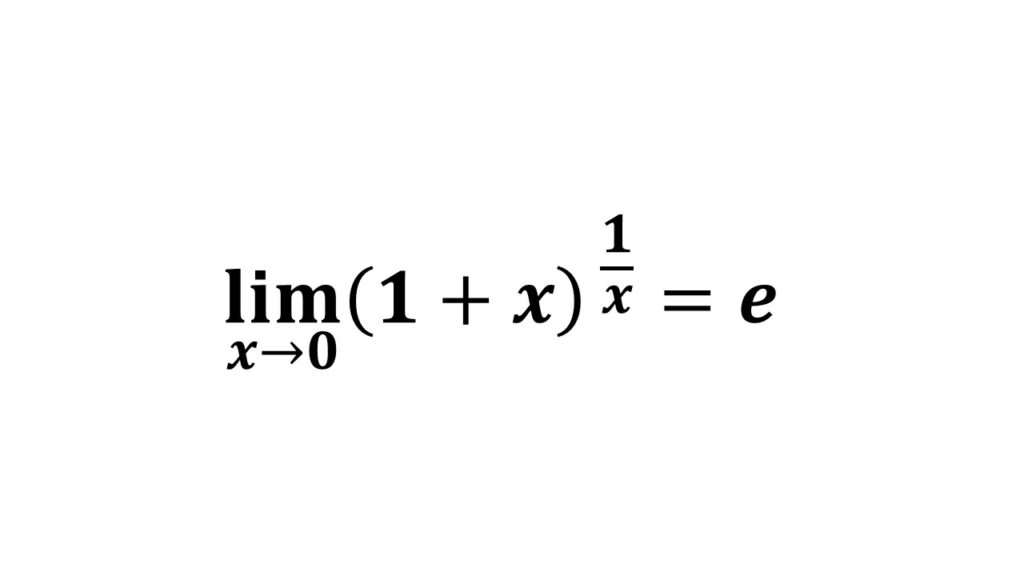
自然対数の底として知られる不思議な定数 e は、約2.71828…で終わりなく続きます。微分や指数関数、対数など、あらゆる数学の分野で大活躍し、「成長」や「変化」の振る舞いをうまく表してくれる頼もしいやつ。複雑な連続複利の計算にも顔を出すことから、経済や金融の世界でも重要な役割を担っています。
第7位:リーマン予想(Riemann Hypothesis)
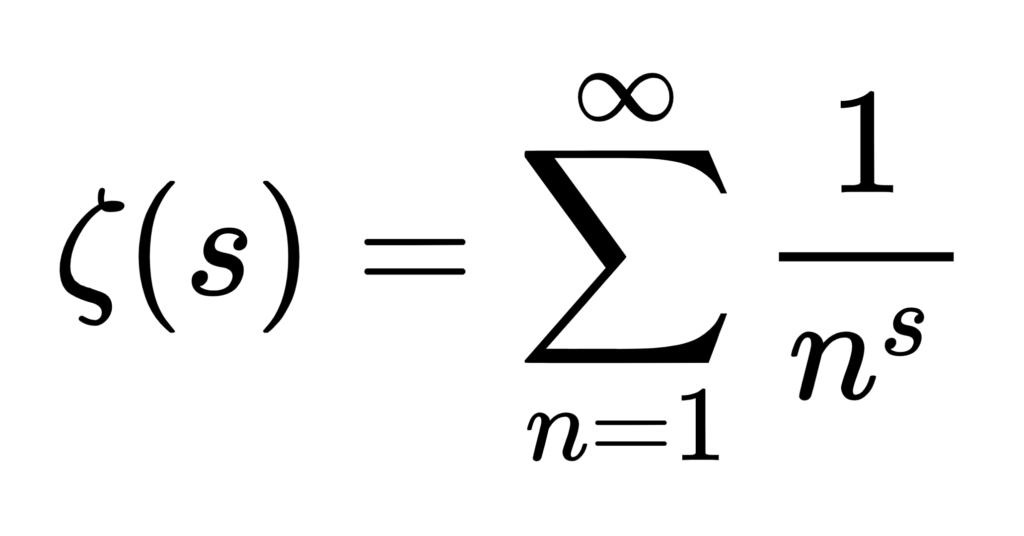
「まだ証明されていないのに、この世で一番有名な予想かも?」といわれるのが、このリーマン予想。素数の分布とゼータ関数という関数の「零点(ゼロになる点)」の位置関係にまつわる、数学史上最大の難問の一つです。その解決には、100万ドルの懸賞金までかけられていますが、いまだに誰も解けず。数学界のロマン漂う存在です。
第6位:スターリングの近似(Stirling’s approximation)
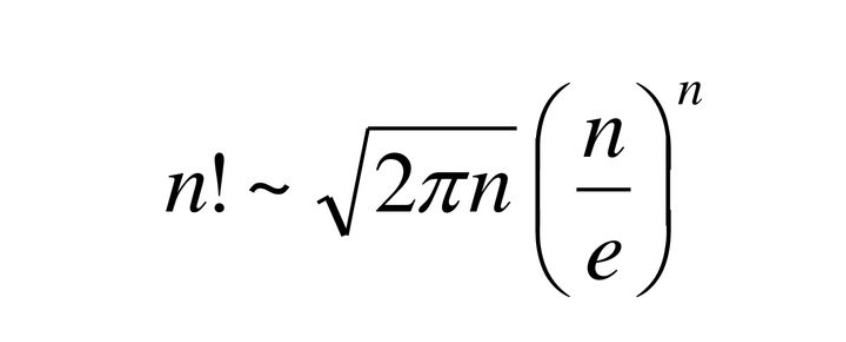
この式は、階乗 𝑛! の大きな値を近似するために使われます。階乗は数が増えるにつれて急激に大きくなりますが、スターリングの近似式を使うことで、その大きさを正確に予測できます。統計学や確率論、物理学の分野でも役立つこの近似式は、大きな数を扱う際の重要なツールです。数の成長を見事に表現するこの式には、数学の深遠な調和が感じられます。
第5位:ピタゴラスの定理 (Pythagorean Theorem)
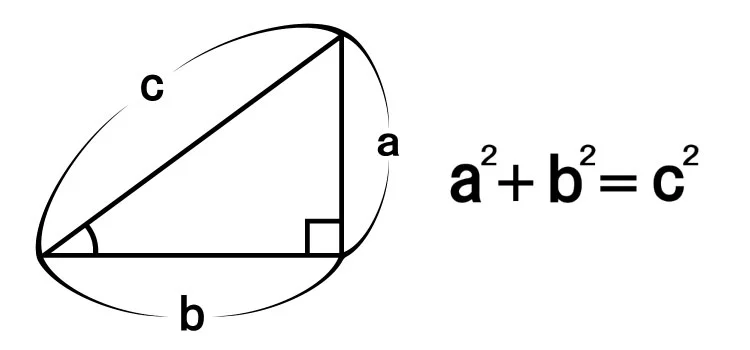
古代ギリシャの数学者ピタゴラスが発見したこの定理は、直角三角形の辺の関係を表しています。長さに着目することで、三角形の美しい対称性とバランスを感じられます。この定理は、幾何学の基本でありながら、現代の数理物理学やコンピュータグラフィックスでも欠かせない重要な役割を果たしています。
第4位:フィボナッチ数 (Fibonacci Sequence)
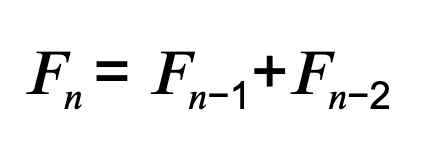
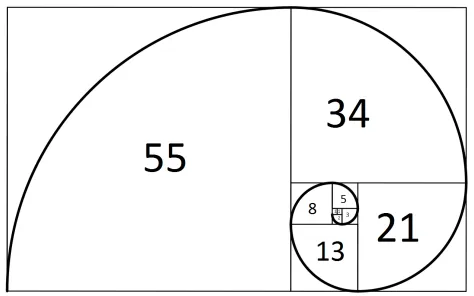
「1, 1, 2, 3, 5, 8, 13, …」と、前の2つの数を足して次の数にしていくという単純なルールなのに、自然界にびっくりするほど登場する不思議な数列。ヒマワリの種の並びや貝殻の渦巻き、葉っぱの配置など、身近な美しさも数学的にとらえられるというのが驚きです。黄金比との関係もあって、芸術や建築にも活かされる、まさに数の神秘の代表格です。
第3位:オイラーの多面体定理 (Euler’s theorem on polyhedra)
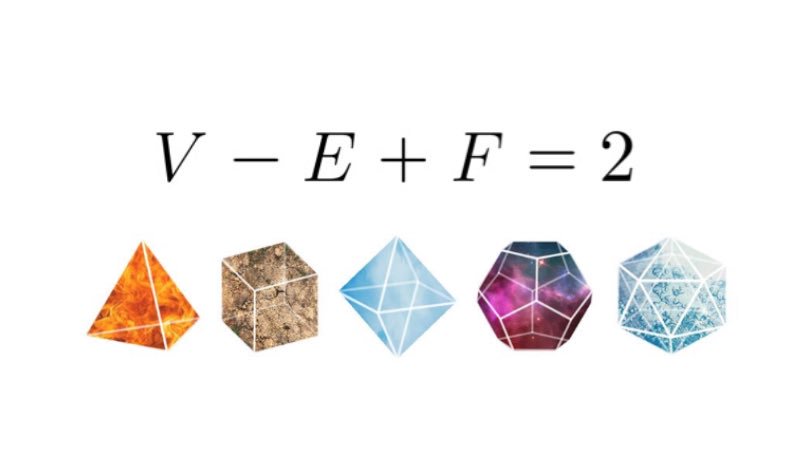
この数式は、立体図形の頂点 (V)、辺 (E)、面 (F) の関係を表しています。どんな多面体でもこの公式が成り立つというシンプルな美しさには驚かされます。幾何学における普遍的な法則を示し、三次元の世界を整然と描き出しています。
第2位:オイラーの等式(Euler’s identity)
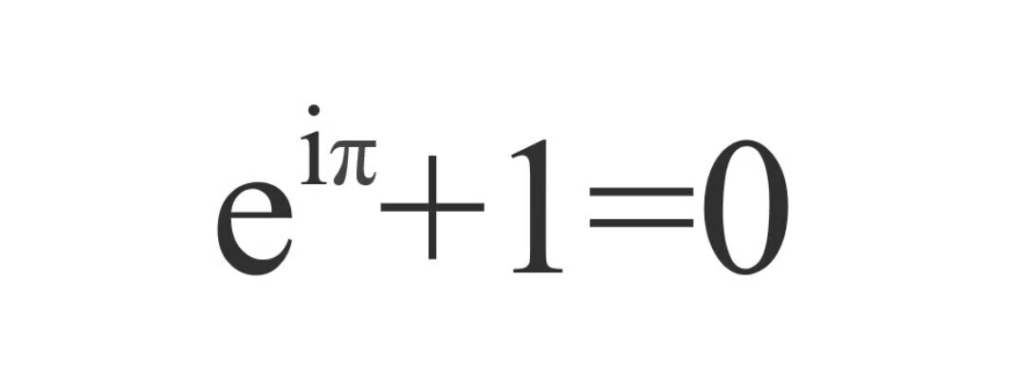
の数式は、まるで魔法のような美しさを持っています。オイラーの等式は、複素数 𝑖 (虚数単位)、自然対数の底 𝑒 、円周率 𝜋 、そして 1 と 0 の五つの基本的な数学的定数をたった一つのシンプルな式で結びつけています。この等式がなぜ成り立つのかを理解するためには複素数の世界を深く探求する必要がありますが、その謎めいた美しさは、多くの数学者が「最も美しい数式」と称賛する理由です。
第1位:質量とエネルギーの等価性 (Mass-Energy Equivalence)
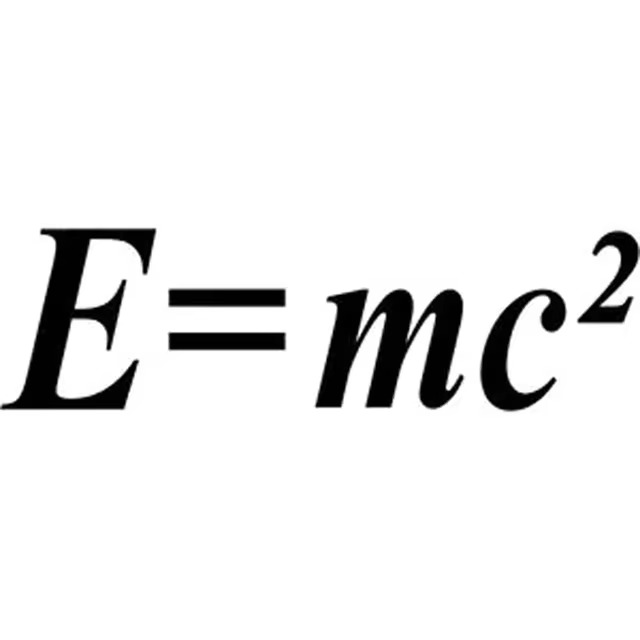
美しい数式ランキング第1位は、アインシュタインの有名な特殊相対性理論から導き出した公式です。この公式は、わずかな質量から巨大なエネルギーが得られることを示しており、核エネルギーや宇宙の進化において決定的な役割を果たしています。シンプルでありながら、宇宙の深淵にまで影響を与えるこの公式は、数式の美しさの頂点にふさわしいと言えるでしょう。
まとめ
いかがでしたでしょうか?数式の美しさは、単に計算の道具としてではなく、自然界の調和や普遍性を映し出す鏡のような存在です。今回紹介した数式たちは、どれも数学や物理学の基盤となるものであり、そのシンプルさや奥深さは時を超えて私たちを魅了し続けます。次に数式を目にするときは、ぜひその「美しさ」にも注目してみてください。きっと新しい視点で世界が広がるはずです。

